Les matrices

INTRODUCTION
Dans le domaine de la programmation 2D/3D, les matrices ont un rôle très importants car elles permettent entre autres de gérer divers effets sur notre monde, comme la translation, la rotation ou encore l'homothétie (facteur de zoom). Ce cours s'appuyera sur la façon dont XNA gère les matrices, mais si vous avez compris ce cours, ce sera très simple de passer à des matrices plus grandes ou plus petites.

COURS

Qu'est-ce qu'une matrice ?

Une matrice est un ensemble de valeurs disposés dans un tableau ayant un certain nombre de lignes et de colonnes. Il existe 3 types de matrices :
- La matrice-colonne : constituée de plusieurs lignes mais ne possédant qu'une colonne.
- La matrice-ligne : constituée de plusieurs colonnes mais ne possédant qu'une ligne.
- La matrice LxC : constituée de plusieurs colonnes et de plusieurs lignes.

Les matrices sous XNA sont des matrices de type LxC dont L et C valent 4. Sous XNA, les lignes et les colonnes sont nommées comme suit :

M11	M12	M13	M14
M21	M22	M23	M24
M31	M32	M33	M34
M41	M42	M43	M44

 Cette façon de nommer les cellules a le mérite d'être clair, car si je veux connaître la valeur de la 3ème ligne, 2ème colonne, j'ai juste à appeler M32.

Addition de matrices

L'addition de matrices est très simple. Imaginons une matrice A et une matrice B. Pour connaitre le résultat AB11, il suffit d'ajouter A11 à B11. Cette matrice montre les calculs à effectuer :

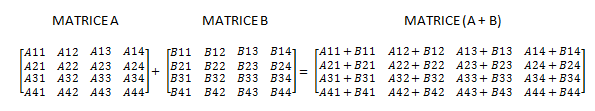
Donc si nous imaginons une matrice A comme ceci :



Et une matrice B, comme ceci :


La matrice résultat vaut :


Soustraction de matrices
La soustraction de matrices fonctionnent exactement comme l'addition de matrices,
remplacez juste + par -.

Pour l'addition et la soustraction, les matrices sont commutatives, c'est à dire que A + B = B + A.

Multiplication de matrices

La multiplication de matrices est plus compliqués car pour connaître le résultat M11 de la matrice résultat, il faut multiplier chaque colonne de la matrice A par la ligne de la matrice B, c'est à dire, effectuer l'opération suivante :
(A11 * B11) + (A12 * B21) + (A13 * B31) + (A14 * B41)

Donc voici le récapitulatif :
RM11 = (A11 * B11) + (A12 * B21) + (A13 * B31) + (A14 * B41)
RM12 = (A11 * B12) + (A12 * B22) + (A13 * B32) + (A14 * B42)
RM13 = (A11 * B13) + (A12 * B23) + (A13 * B33) + (A14 * B43)
RM14 = (A11 * B14) + (A12 * B24) + (A13 * B34) + (A14 * B44)

RM21 = (A21 * B11) + (A22 * B21) + (A23 * B31) + (A24 * B41)
RM22 = (A21 * B12) + (A22 * B22) + (A23 * B32) + (A24 * B42)
RM23 = (A21 * B13) + (A22 * B23) + (A23 * B33) + (A24 * B43)
RM24 = (A21 * B14) + (A22 * B24) + (A23 * B34) + (A24 * B44)

RM31 = (A31 * B11) + (A32 * B21) + (A33 * B31) + (A34 * B41)
RM32 = (A31 * B12) + (A32 * B22) + (A33 * B32) + (A34 * B42)
RM33 = (A31 * B13) + (A32 * B23) + (A33 * B33) + (A34 * B43)
RM34 = (A31 * B14) + (A32 * B24) + (A33 * B34) + (A34 * B44)

RM41 = (A41 * B11) + (A42 * B21) + (A43 * B31) + (A44 * B41)
RM42 = (A41 * B12) + (A42 * B22) + (A43 * B32) + (A44 * B42)
RM43 = (A41 * B13) + (A42 * B23) + (A43 * B33) + (A44 * B43)
RM44 = (A41 * B14) + (A42 * B24) + (A43 * B34) + (A44 * B44)

Maintentant, 2 petits exemples, prenons la matrice A, qui est définie comme ceci :
   
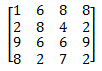
et la matrice B, définie comme ceci :

Nous allons effectuer le calcul R = A * B, nous aurons donc :

R11 = (1 * 7) + (6 * 0) + (8 * 6) + (8 * 9) = 7 + 0 + 48 + 72 = 127
R12 = (1 * 1) + (6 * 1) + (8 * 8) + (8 * 7) = 1 + 6 + 64 + 56 = 127
R13 = (1 * 1) + (6 * 6) + (8 * 1) + (8 * 7) = 1 + 36 + 8 + 56 = 101
R14 = (1 * 6) + (6 * 3) + (8 * 9) + (8 * 2) = 6 + 18 + 72 + 16 = 112

R21 = (2 * 7) + (8 * 0) + (4 * 6) + (2 * 9) = 14 + 0 + 24 + 18 = 56
R22 = (2 * 1) + (8 * 1) + (4 * 8) + (2 * 7) = 2 + 8 + 32 + 14 = 56
R23 = (2 * 1) + (8 * 6) + (4 * 1) + (2 * 7) = 2 + 48 + 4 + 14 = 68
R24 = (2 * 6) + (8 * 3) + (4 * 9) + (2 * 2) = 12 + 24 + 36 + 4 = 76

R31 = (9 * 7) + (6 * 0) + (6 * 6) + (9 * 9) = 63 + 0 + 36 + 81 = 180
R32 = (9 * 1) + (6 * 1) + (6 * 8) + (9 * 7) = 9 + 6 + 48 + 63 = 126
R33 = (9 * 1) + (6 * 6) + (6 * 1) + (9 * 7) = 9 + 36 + 6 + 63 = 114
R34 = (9 * 6) + (6 * 3) + (6 * 9) + (9 * 2) = 54 + 18 + 54 + 18 = 144

R41 = (8 * 7) + (2 * 0) + (7 * 6) + (2 * 9) = 56 + 0 + 42 +  18 = 116
R42 = (8 * 1) + (2 * 1) + (7 * 8) + (2 * 7) = 8 + 2 + 56 + 14 = 80
R43 = (8 * 1) + (2 * 6) + (7 * 1) + (2 * 7) = 8 + 12 + 7 + 14 = 41
R44 = (8 * 6) + (2 * 3) + (7 * 9) + (2 * 2) = 48 + 6 + 63 + 4 = 121

Maintenant effectuons le calcul S = B * A, nous aurons donc :


S11 = (7 * 1) + (1 * 2) + (1 * 9) + (6 * 8) = 7 + 2 + 9 + 48 = 66
S12 = (7 * 6) + (1 * 8) + (1 * 6) + (6 * 2) = 42 + 8 + 6 + 12 = 68
S13 = (7 * 8) + (1 * 4) + (1 * 6) + (6 * 7) = 56 + 4 + 6 + 42 = 108
S14 = (7 * 8) + (1 * 2) + (1 * 9) + (6 * 2) = 56 + 2 + 9 + 12 = 79

S21 = (0 * 1) + (1 * 2) + (6 * 9) + (3 * 8) = 0 + 2 + 54 + 24 = 80
S22 = (0 * 6) + (1 * 8) + (6 * 6) + (3 * 2) = 0 + 8 + 36 + 6 = 50
S23 = (0 * 8) + (1 * 4) + (6 * 6) + (3 * 7) = 0 + 4 + 36 + 21 = 61
S24 = (0 * 8) + (1 * 2) + (6 * 9) + (3 * 2) = 0 + 2 + 54 + 6 = 62

S31 = (6 * 1) + (8 * 2) + (1 * 9) + (9 * 8) = 6 + 16 + 9 + 72 = 103
S32 = (6 * 6) + (8 * 8) + (1 * 6) + (9 * 2) = 36 + 64 + 6 + 18 = 124
S33 = (6 * 8) + (8 * 4) + (1 * 6) + (9 * 7) = 48 + 32 + 6 + 63 = 149
S34 = (6 * 8) + (8 * 2) + (1 * 9) + (9 * 2) = 48 + 16 + 9 + 18 = 91

S41 = (9 * 1) + (7 * 2) + (7 * 9) + (2 * 8) = 9 + 14 + 63 + 16 = 102
S42 = (9 * 6) + (7 * 8) + (7 * 6) + (2 * 2) = 54 + 56 + 42 + 4 = 156
S43 = (9 * 8) + (7 * 4) + (7 * 6) + (2 * 7) = 72 + 28 + 42 + 14 = 156
S44 = (9 * 8) + (7 * 2) + (7 * 9) + (2 * 2) = 72 + 14 + 63 + 4 = 153

Comme nous pouvons le constater A * B est différent de B * A. Cela veut donc dire que les multiplications de matrices ne sont pas commutatives. C'est très important car lorsque vous voudrez effectuer des transformations sur votre monde, il ne faudra pas faire n'importe quoi !!!

Division de matrices

La division de matrices respecte le même schéma que la multiplication de matrices, remplacez juste le signe * par /.

Matrice Identité

La matrice Identité est très simple à comprendre puisqu'elle vaut ceci :

1	0	0	0
0	1	0	0
0	0	1	0
0	0	0	1

Matrice de translation

La matrice de translation est définie ainsi :

1	0	0	X
0	1	0	Y
0	0	1	Z
0	0	0	1

Matrice de rotation

Il existe une matrice de rotation pour chacun des 3 axes (X, Y, et Z)

La matrice de rotation sur l'axe X est définie comme suit :

1	0	0	0
0	Cos(angle)	Sin(angle)	0
0	-Sin(angle)	Cos(angle)	0
0	0	0	1

La matrice de rotation sur l'axe Y est définie comme suit :

Cos(angle)	0	Sin(angle)	0
0	1	0	0
-Sin(angle)	0	Cos(angle)	0
0	0	0	1

La matrice de rotation sur l'axe Z est définie comme suit :

Cos(angle)	Sin(angle)	0	0
-Sin(angle)	Cos(angle)	0	0
0	0	1	0
0	0	0	1

Nota : angle est l'angle de rotation en degrés.

Matrice d'homothétie

La matrice d'homothétie est définie par :

Sx	0	0	0
0	Sy	0	0
0	0	Sz	0
0	0	0	1

Combiner diverses transformation de matrices

Dans un jeu vidéo, nous effectuons les transformations dans cette ordre :
- repositionner l'objet à son origine.
- effectuer l'homothétie.
- effectuer la rotation.
- repositionner l'objet à sa position sur l'écran.

Pourquoi effectuer les choses dans cet ordre ? Eh bien, imaginez un cercle. Sur ce cercle vous mettez un objet à un endroit quelquonque. L'objet est symbolisé par le trait rouge.


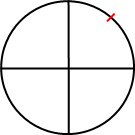
Nous voulons tourner cette objet de 90 degrés. Le centre du cercle correspond au centre de rotation.  Si nous n'effectuons pas la première étape, voici ce que donne la rotation.


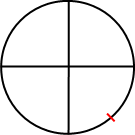
Donc maintenant nous savons pourquoi l'objet doit être repositionné. Mais si nous le repositionnons, et que nous appliquons la rotation, l'objet restera à la position de rotation, donc il nous faudra le repositionner à l'écran.

Cet article est terminé. Le prochain s'occupera de créer une caméra 2D pour un jeu XNA et celui d'après de créer un petit exemple d'utilisation de cette caméra.

Stay tuned,

@bientôt sur ce blog